Первым человеком, предположившим шарообразную форму нашей планеты, был древнегреческий математик и философ Пифагор (570 – 490 годы до нашей эры). Его идея о вращении Земли вокруг оси в течение суточного периода, а за год вокруг Солнца, получила научное подтверждение польским астрономом Николаем Коперником (1473-1543). Его учение о гелиоцентрической системе стала своего рода началом первой научной революции.
Выдающимся событием следует считать деятельность персидского астронома, математика, геодезиста и философа Аль-Бируни (973-1048годы). В области геодезии он производил расчеты по определению радиуса Земли. Удивительные результаты вычислений Аль-Бируни получил при определении длины дуги меридиана угловой величиной в один градус на 32 параллели северной широты значением в 110,278км. При современных измерениях были получены линейные значения дуги в 110,895км.
Эти яркие события по определению формы и размеров Земли, измерениям на ее поверхности характерны по своему предмету исследований учеными в первый период развития геодезии.
Началом второго этапа в эволюционировании геодезической науки считаются времена морских путешествий и географических открытий: четырех экспедиций в Америку Христофора Колумба (1492-1504), трех мореплаваний в Индию Васко да Гама (1497-1524), кругосветки Фернана Магеллана (1519-1522).
В это период происходят важнейшие изобретения в геодезии:
• зрительной трубы итальянца Галилея (1609 год);
• метода триангуляции нидерландца Снелиусса (1614 год);
• первое применение сетки нитей в приборах французом Пикаром;
• выход в свет научного труда англичанина Ньютона, в котором теоретически обосновывается полюсное сжатие и определяется его величина.
Третий период характерен разрешением многих геодезических задач:
• нахождением размеров эллипсоида Земли;
• определением геоида;
• математической обработки измерений различными методами наименьших квадратов;
• возникновением новых геодезических приборов, новых направлений наук геофизики, гравиметрии;
• определения фигуры физической поверхности Земного шара.
В современный период значительным продвижением в геодезической отрасли являются использование спутниковых технологий, появление глобальных навигационных систем позиционирования, новых физических методов измерений, геоинформационных и компьютерных систем.
Что изучает геодезия
Современная геодезия представляет собой многогранную отрасль, которые складываются в результате научных и учебно-методических отношений, производственных и технологических процессов между частными лицами и юридическими субъектами, государственными учреждениями и различными организациями, занимающимися вопросами, связанными с деятельностью по изучению, использованию земной поверхности Земли в различных направлениях и обязательному геодезическому контролю.
Предметом изучения геодезической науки служит:
• формы Земли, с периодическими определениями их размеров;
• физическая поверхность Земли с выполнением на ней измерений;
• геодинамических процессов, происходящих в земной поверхности;
• определение действия сил тяжести Земли в разных ее точках;
• установление точек и систем отсчета, координат для всей территории государства и планеты, требующихся для единого пространственного положения с целью решения системных планетарных задач разностороннего характера;
• математические методы построения геодезических сетей для формирования единства систем координат на земной поверхности;
• физические и математические способы геодезических измерений;
• математических методов обработки полевых измерений и теоретических уравнительных их вычислений.
Основные задачи геодезии
Невозможно представить себе ни одного хозяйствующего субъекта, ни одну область экономики без присутствия и участия в них практической геодезии. По правде сказать, многие из них не подозревают или не знают о такой связи. Главное, что геодезическая отрасль востребована и решает многие практические задачи:
• создания пунктов геодезических сетей разного уровня тем самым формирую государственную систему координат;
• исполнения топографических съемок для изыскательских и картографических работ;
• составления карт и топографических планов;
• обеспечения геодезических процессов при строительстве объектов материального производства;
• определения геодезическими способами деформаций грунта, просадок, сдвига фундаментов и крена конструкций сооружений;
• геодезическо-маркшейдерское обслуживание подземных и открытых горных работ в шахтах и рудниках, карьерах и полигонах;
• исследования и разведки природных ресурсов и полезных ископаемых;
• при ведении землеустроительных работ и кадастрового учета;
• обеспечение космической, воздушной, наземной и морской навигаций всевозможных летательных аппаратов, кораблей и автомобильной техники.
Занимательная геодезия
Всем привет!
Сегодня я расскажу тебе, о координатах, проекциях, геодезических системах и совсем чуть-чуть о веб-картографии. Устраивайся поудобнее.
Как говорил ещё Артур Кларк, любая достаточно развитая технология неотличима от магии. Так и в веб-картографии — я думаю, все давно привыкли пользоваться географическими картами, но далеко не каждый представляет себе, как это всё работает.
Вот, казалось бы, простая вещь — географические координаты. Широта и долгота, что может быть проще. А вот представьте, что вы очутились на необитаемом острове. Смартфон утонул, а других средств связи у вас нет. Остаётся только написать письмо с просьбой о помощи и по старинке выбросить его в море в запечатанной бутылке.
Вот только незадача — вы совершенно не знаете, где находится ваш необитаемый остров, а без указания координат никто вас не найдёт, даже если выловит ваше письмо. Что делать? Как определить координаты без GPS?
Итак, немного теории для начала. Чтобы сопоставить точкам на поверхности сферы координаты, необходимо задать начало отсчета — фундаментальную плоскость для отсчёта широт и нулевой меридиан для отсчёта долгот. Для Земли обычно используются плоскость экватора и гринвичский меридиан соответственно.
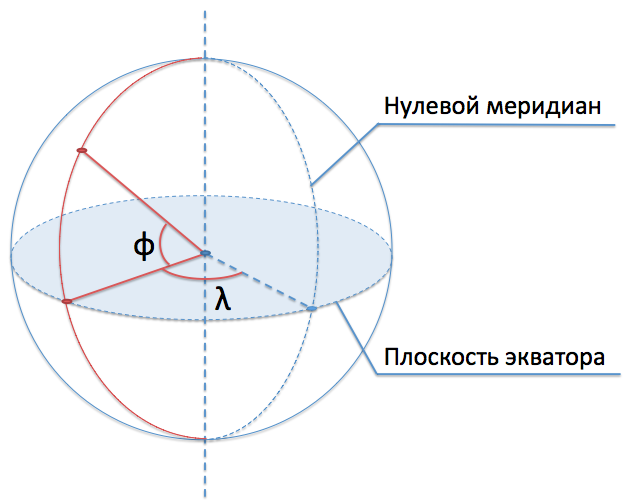
Широтой (обычно обозначается φ) называют угол между направлением на точку из центра сферы и фундаментальной плоскостью. Долготой (обычно обозначается θ или λ) называют угол между плоскостью проходящего через точку меридиана и плоскостью нулевого меридиана.
Как же определить свою широту, т.е. угол между плоскостью земного экватора и точкой, в которой ты находишься?
Посмотрим на тот же чертёж под другим углом, спроецировав его на плоскость нашего меридиана. Добавим также к чертежу плоскость горизонта (касательную плоскость к нашей точке):
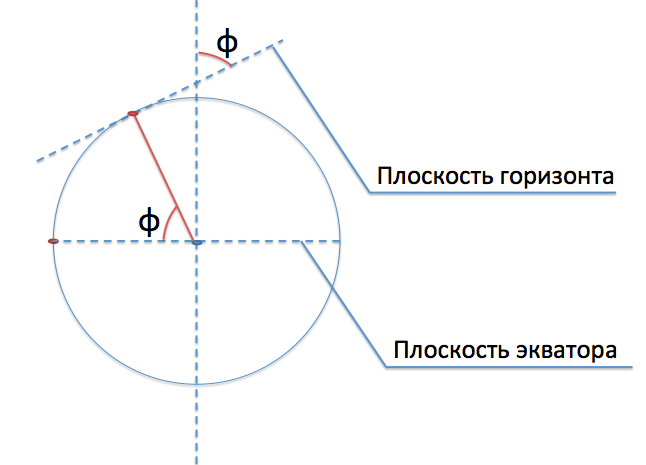
Видим, что искомый угол между направлением на точку и плоскостью экватора равен углу между плоскостью горизонта и осью вращения Земли.
Итак, как же нам найти этот угол? Вспомним красивые картинки звёздного неба с большой выдержкой:

Вот эта точка в центре всех описываемых звездами окружностей — полюс мира. Измерив её высоту над горизонтом, мы получим широту точки наблюдения.
Остаётся вопрос, как найти полюс мира на звёздном небе. Если вы в Северном полушарии, то всё довольно просто:
— найдите ковш Большой Медведицы;
— проведите мысленно прямую через две крайние звезды ковша — Дубхе и Мерак;
— эта прямая укажет вам на ручку ковша Малой Медведицы. Крайняя звезда этой ручки — Полярная — почти в точности совпадает с Северным Полюсом мира.
Полярная звезда всегда находится на севере, а её высота над горизонтом равна широте точки наблюдения. Если вас угораздит попасть на Северный полюс, Полярная звезда будет у вас точно над головой.
В Южном полушарии всё не так просто. Рядом с южным полюсом мира нет крупных звёзд, и вам придётся найти созвездие Южный Крест, мысленно продлить вниз его бОльшую перекладину и отсчитать 4.5 её длины — где-то в этой области будет находиться южный полюс мира.
Само созвездие найти легко — вы много раз видели его на флагах разных стран — Австралии, Новой Зеландии и Бразилии, например.

С широтой определились. Перейдём к долготе. Как определить долготу на необитаемом острове?
На самом деле, это очень непростая проблема, потому что, в отличие от широты, точка отсчета долготы (нулевой меридиан) выбирается произвольным образом и ни к каким наблюдаемым ориентирам не привязана. Испанский король Филипп II в 1567 году назначил солидное вознаграждение тому, кто предложит метод определения долготы; в 1598 году при Филиппе III оно доросло до 6 тысяч дукатов единовременно и 2 тысячи дукатов ренты пожизненно — очень приличная сумма по тем временам. Задача определения долготы в течение нескольких десятилетий была идеей фикс математиков, как теорема Ферма в 20-м веке.
В итоге, долготу стали определять с помощью вот этого прибора:

По сути, этот прибор остаётся самым надёжным способом определения долготы (не считая GPS/Глонасс) и в наши дни. Этот прибор… (барабанная дробь)…морской хронометр.
В самом деле, при изменении долготы меняется часовой пояс. По разнице локального времени и гринвичского легко определить собственную долготу, причём очень точно. Каждая минута разницы времён соответствует 15 угловым минутам долготы.
Соответственно, если у вас есть часы, настроенные по гринвичскому времени (на самом деле, неважно по какому — достаточно знать часовой пояс того места, по времени которого идут ваши часы) — не спешите их переводить. Дождитесь местного полдня, и разница времён подскажет вам долготу вашего острова. (Определить момент полдня очень легко — следите за тенями. В первой половине дня тени укорачиваются, во второй — удлиняются. Момент, когда начали удлиняться тени — астрономический полдень в данной местности.)
Оба метода определения координат, кстати, хорошо описаны в романе Жюля Верна «Таинственный остров».


